

We can rewrite the right-hand side of our equation such that Let 𝑇 = 7 2 9.Īnd 𝑟 is the common ratio between terms: We define the first term of a geometric sequence as 𝑇. Term is 1, and sum of all terms is 1 093 is. Number of terms in a particular geometric sequence.Įxample 3: Finding the Number of Terms of a Finite Geometric Sequence given Its Sumįill in the blank: The number of terms of a geometric sequence whose first term is 729, last In our next example, we will need to rearrange our formulae to calculate the The sum of the geometric sequence 1 6, − 3 2, 6 4, …, 2 5 6 To find the sum of the series, we can now use the The formula for the 𝑛 t h term of a geometric The common ratio of the sequence is equal to − 2. We can calculate the value of the common ratio, 𝑟,īy dividing any term by the term that precedes it:
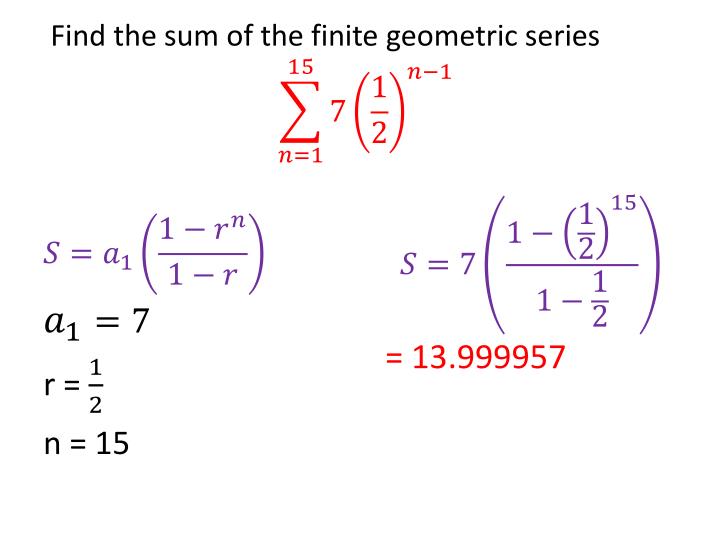

Īlternatively, we could have subtracted (1)Įxample 2: Finding the Sum of a Finite Geometric Sequence įactoring 𝑆 from the right-hand side and If we multiply both sides of our equation by 𝑟, we have So the sum of the first 𝑛 terms of a geometric We will now derive a formula for the sum of the first 𝑛Ĭonsider a geometric sequence with first term 𝑇Īnd common ratio 𝑟. We can see that the sum of these terms is 59 048. In this case, by adding together the first 10 terms in the series, The sum of the terms in a sequence is called a series. Of multiplying the previous term by the common ration, we find that Since we multiply one term by the common ratio to get the next term,Īnd by dividing both sides of the equation byĪlternatively, with the definition that one term is the result


 0 kommentar(er)
0 kommentar(er)
